The 30–60–90 Day Plan is a document prepared by a job seeker and presented during an interview It is an outline of what the candidate intends or proposes to achieve in the first 90 days, if hired for the role Beside above, what are the sides of a 30 60 90 Triangle?30 60 And 90 Triangle Rule The Complete Guide to the Triangle How To Work With degree Triangles Education Is Around トップ 100 30 60 90 Triangle サゴタケモAn equilateral triangle with side lengths of 2 cm can be used to find exact values for the trigonometric ratios of 30° and 60° The equilateral triangle can be
Pythagoras Theorem On 30 60 90 Triangle Youtube
45 45 90 and 30 60 90 triangle rules
45 45 90 and 30 60 90 triangle rules- A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherWatch more videos on http//wwwbrightstormcom/math/geometrySUBSCRIBE FOR All OUR VIDEOS!https//wwwyoutubecom/subscription_center?add_user=brightstorm2VI




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube
30 60 90 Triangle Rules Unit Circle Triangles Theorem 2 In a triangle whose angles measure 30 0, 60 0, and 90 , the hypotenuse has a length 0 equal to twice the length of the shorter leg, and the length of the longer leg is the product of 3 And the length of the shorter leg The ratio of the sides of a triangle are x x 3 2 x Note The short leg is alwaysIn any triangle, you see the following The shortest leg is across from the 30degree angle, the length of the hypotenuse is always double the length of the shortest leg, and you can find the length of the long leg by multiplying the short leg by the square root of 3A 30 60 90 triangle completes an arithmetic progression 3030=6030 =90 An arithmetic progression is a sequence of numbers in which the difference of any two successive numbers is a constant For instance, 2,4,6,8 is an arithmetic progression with a constant of 2
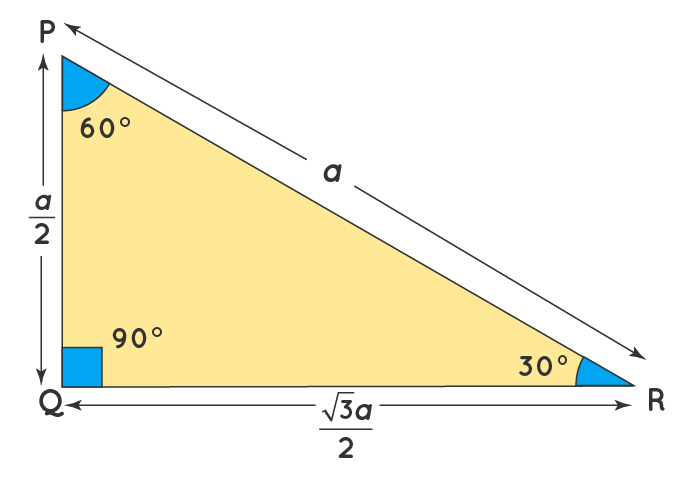
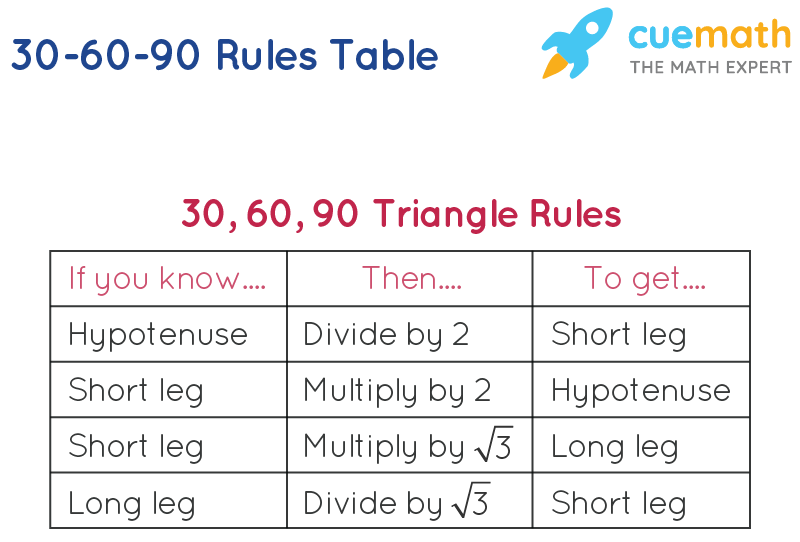
The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x Long side (opposite the 60 60 degree angle) = x√3 x 3Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math 90 60 30 Triangle Rule, Special Right Triangle 30 60 90 Lesson Basic Geometry Concepts Pythagorean Theorem And Special Right Triangles Diagram Quizlet Tips for Remembering the Rules Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is
Printable stepbystep instructions for drawing a triangle with compass and straightedge or ruler Math Open Reference Home Contact About Subject Index Constructing a triangle This is the stepbystep, printable version If you tan (60) = √3/1 = 173 The right triangle is special because it is the only right triangle whose angles are a progression of integer multiples of a single angle If angle A is 30 degrees, the angle B = 2A (60 degrees) and angle C = 3A (90 degrees) Tips for Remembering the Rules Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°) READ How do you win a retaliation lawsuit against an employer?



The Easy Guide To The 30 60 90 Triangle



Special Right Triangles
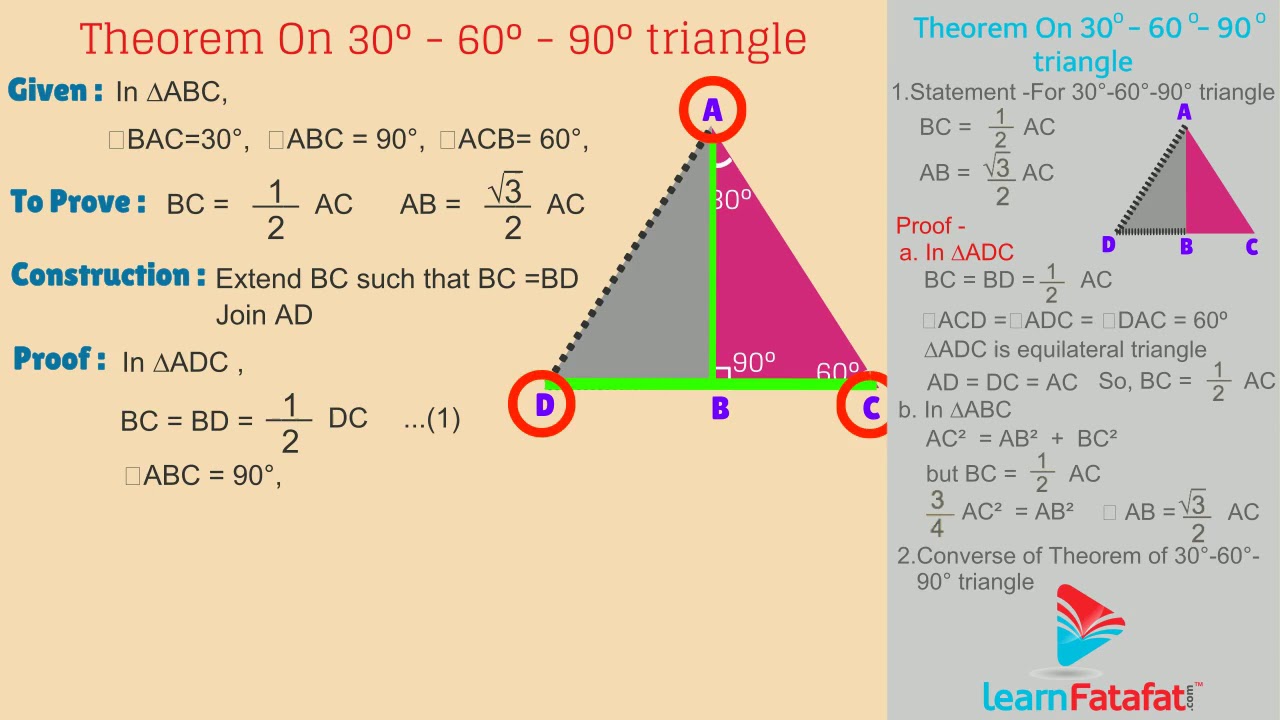
Here is the proof that in a 30°60°90° triangle the sides are in the ratio 1 2 It is based on the fact that a 30°60°90° triangle is half of an equilateral triangle Draw the equilateral triangle ABC Then each of its equal angles is 60° (Theorems 3 and 9) Draw the straight line AD bisecting the angle at A into two 30° anglesTips for Remembering the Rules Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°)30 60 90 triangle rules In a triangle, the rule is The picture shows that the 90 is 12 Than it means 2x=12 For 30 or side s we need x which is 6 For 60 the answer is The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



Special Right Triangle 30 60 45 45 37 53 Elearning
A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one anotherAs one angle is 90, so this triangle is always a right triangle As explained above that it is a special triangle so it has special values of lengths and angles The basic triangle sides ratio is The side opposite the 30° angle x The side oppositeA triangle is a right triangle with angle measures of 30º, 60º




The 30 60 90 Triangle Topics In Trigonometry




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet
The triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 123 Here, a right triangle means being any triangle that contains a 90° angle A triangle is a special right triangle that always has angles of measure 30°, 60°, and 90° Simplify {eq}A=x^ {2}\sqrt {3} {/eq} Thus, for a triangle, the formula for the area is {eq}A=x^ {2}\sqrt {3} {/eq} The Pythagorean Theorem The triangle is a special right triangle, and knowing it can save you a lot of time on standardized tests like the SAT and ACT Because its angles and side ratios are consistent, test makers love to incorporate this triangle into problems, especially on the nocalculator portion of




30 60 90 Triangle Theorem Ratio Formula Video



30 60 90 Triangle Definition Theorem Formula Examples
Tips for Remembering the Rules Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°)The 45 45 90 triangle theorem states that 45 45 90 special right triangles that have sides of which the lengths are in a special ratio of 1 1 2 11sqrt{2} 112 and two 4 5 45 45° angles and one right a/c = sin (30°) = 1/2 so c = 2a b/c = sin (60°) = √3/2 so b = c√3/2 = a√3 Also, if you know two sides of the triangle, you can find the third one from the Pythagorean theorem However, the methods described above are more useful as they need to have only one side of the 30 60 90 triangle given



30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures
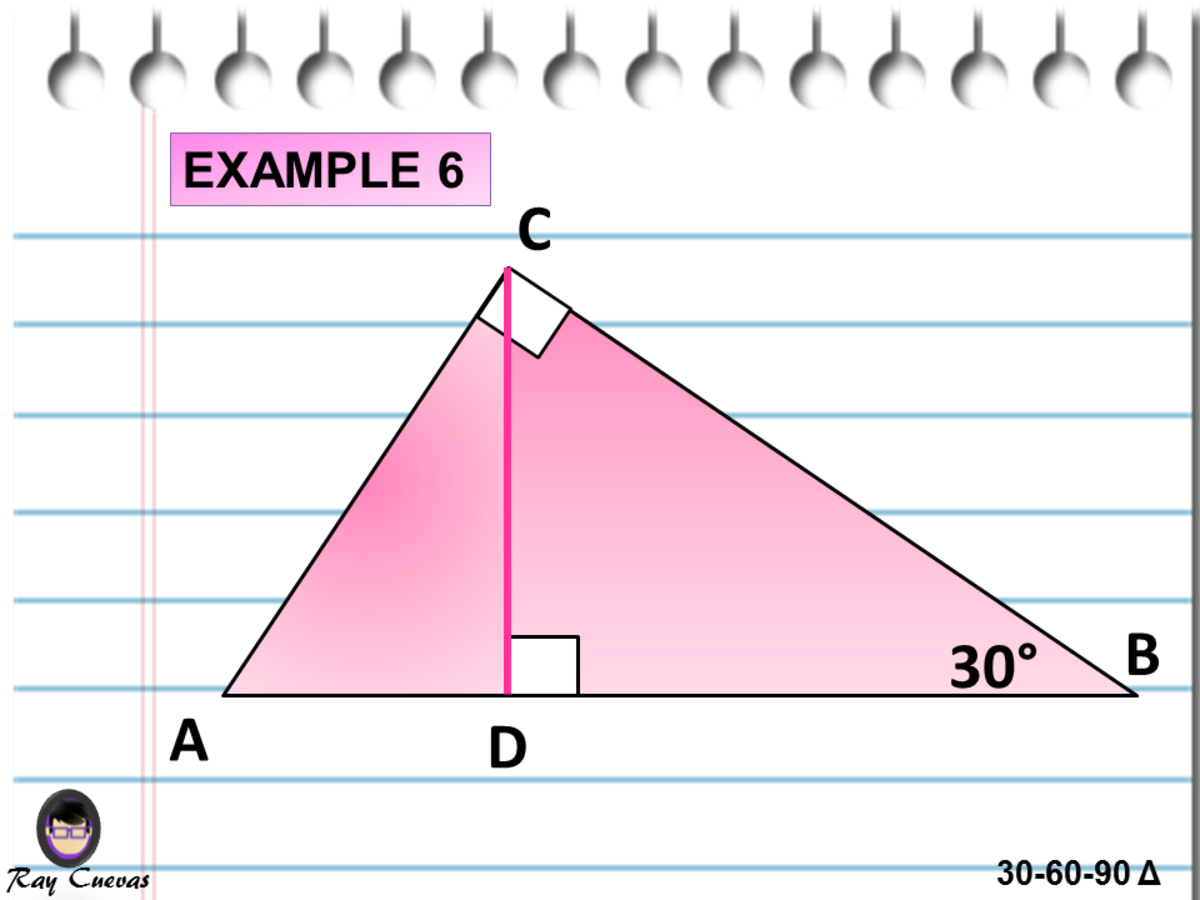



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
30 60 90 Triangle Rules To fully solve our right triangle as a 30 60 90, we have to first determine that the 3 angles of the triangle are 30, 60, and 90 To solve for the side lengths, a minimum of 1 side length must already be known If we know that we are working with a right triangle, we know that one of the angles is 90 degreesThe other triangle is named a triangle, where the angles in the triangle are 30 degrees, 60 degrees, and 90 degrees Secondly, what are the side lengths of a 45 45 90 Triangle?A triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangle




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Definition Theorem Formula Examples
It doesn't matter whichThe sides of a right triangle lie in the ratio 1√32 The side lengths and angle measurements of a right triangle Credit Public Domain We can see why these relations should hold by plugging in the above values into the Pythagorean theorem a2 b2 = c2 a2 ( a √3) 2 = (2 a) 2 a2 3 a2 = 4 a2 A triangle is a special right triangle (a right triangle being any triangle that contains a 90 degree angle) that always has degree angles of 30 degrees, 60 degrees, and 90 degrees Because it is a special triangle, it also has side length values which are always in a consistent relationship with one another




30 60 90 Triangle Theorem Ratio Formula Video
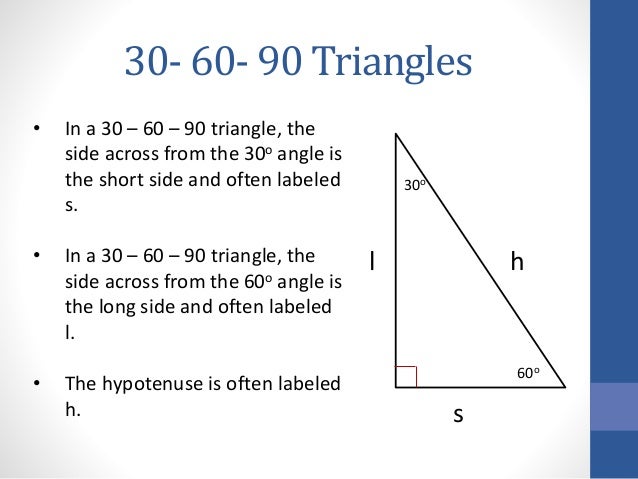



30 60 90 Triangles
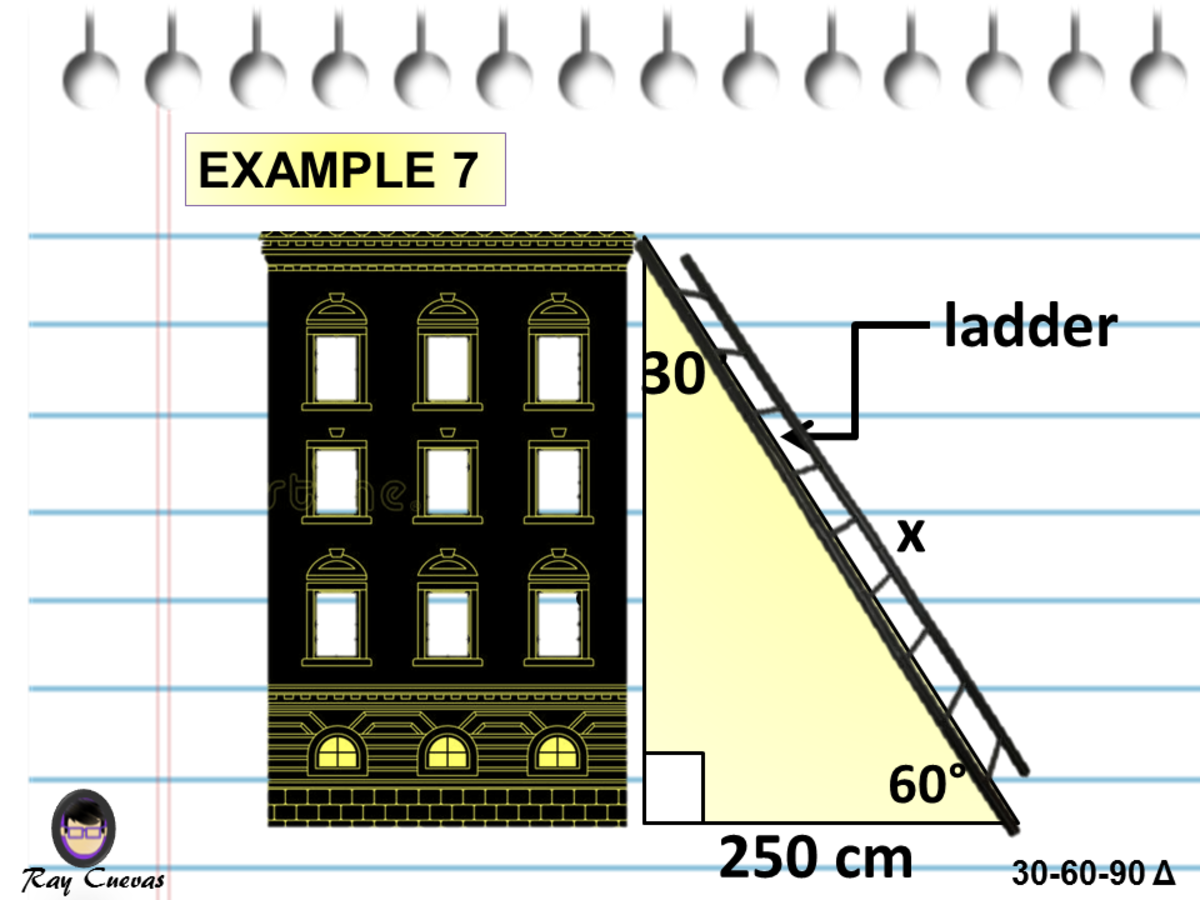
30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2The 30 60 90 right triangle is a special case triangle with angles measuring 30 60 and 90 degrees 30 60 90 triangle in trigonometry And because this is a 30 60 90 triangle and we were told that the shortest side is 8 the hypotenuse must be 16 and the missing side must be 8 3 or 8 3 What is the Triangle rule?
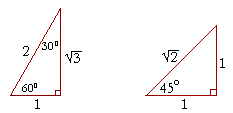



The 30 60 90 Triangle Topics In Trigonometry




Objective To Use The Properties Of 30 60 90 Triangle Ppt Download
Tips for Remembering the Rules Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°) What is the Triangle rule?Right Triangle Calculator Although all right triangles have special features – trigonometric functions and the Pythagorean theorem The most frequently studied right triangles , the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles



Right Triangles Gmat Free
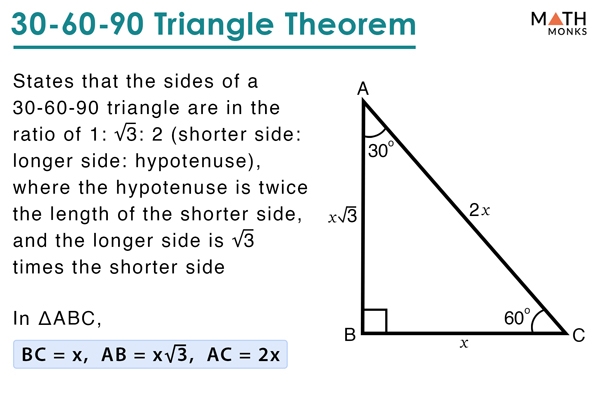



30 60 90 Triangle Definition Formulas Examples
Tips for Remembering the Rules Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°)The triangle is also a right triangle The Formulas of the Given that X is the shortest side measure, we know we can measure out at the baseline for length X , turn an angle of 60 degrees, and have a new line that eventually intersects the line from the larger side atThis rule only works for right triangles whose other internal angles are 30° and 60° respectively Further, for the rule to work, you need to know the length of one side;




30 60 90 Triangles




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
Answer (1 of 3) How do I find the missing sides in special right triangles using the 30–60–90 rule?




30 60 90 Right Triangles Ck 12 Foundation




30 60 90 Triangle Explanation Examples



Solve A 30 60 90 Triangle With Gradea




30 60 90 Triangles Spock S Guide To Math 4




The Complete Guide To The 30 60 90 Triangle




How To Use The Special Right Triangle 30 60 90 Studypug
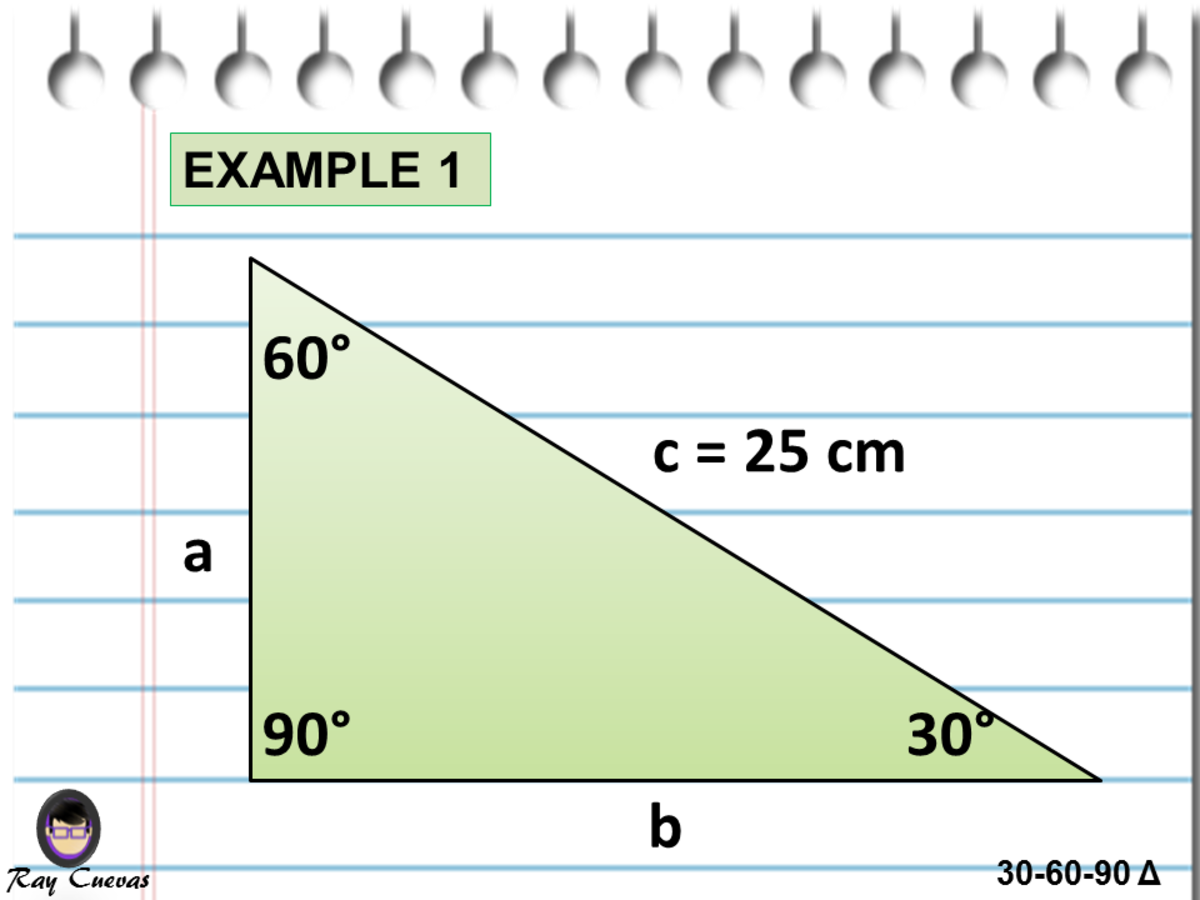



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



1




30 60 90 Triangles
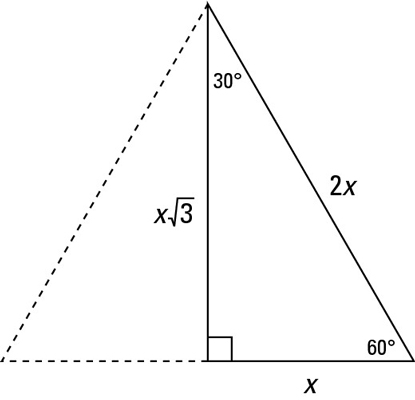



Identifying The 30 60 90 Degree Triangle Dummies



Special Right Triangles Proof




Foundation Class X Theorem Of 30 60 90 Triangle In Marathi Offered By Unacademy



The Easy Guide To The 30 60 90 Triangle




Pythagoras Theorem On 30 60 90 Triangle Youtube



Solve A 30 60 90 Triangle With Gradea



5 5 Special Triangles




Special Right Triangles Fully Explained W 19 Examples
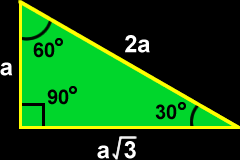



The Geometry Of Triangles
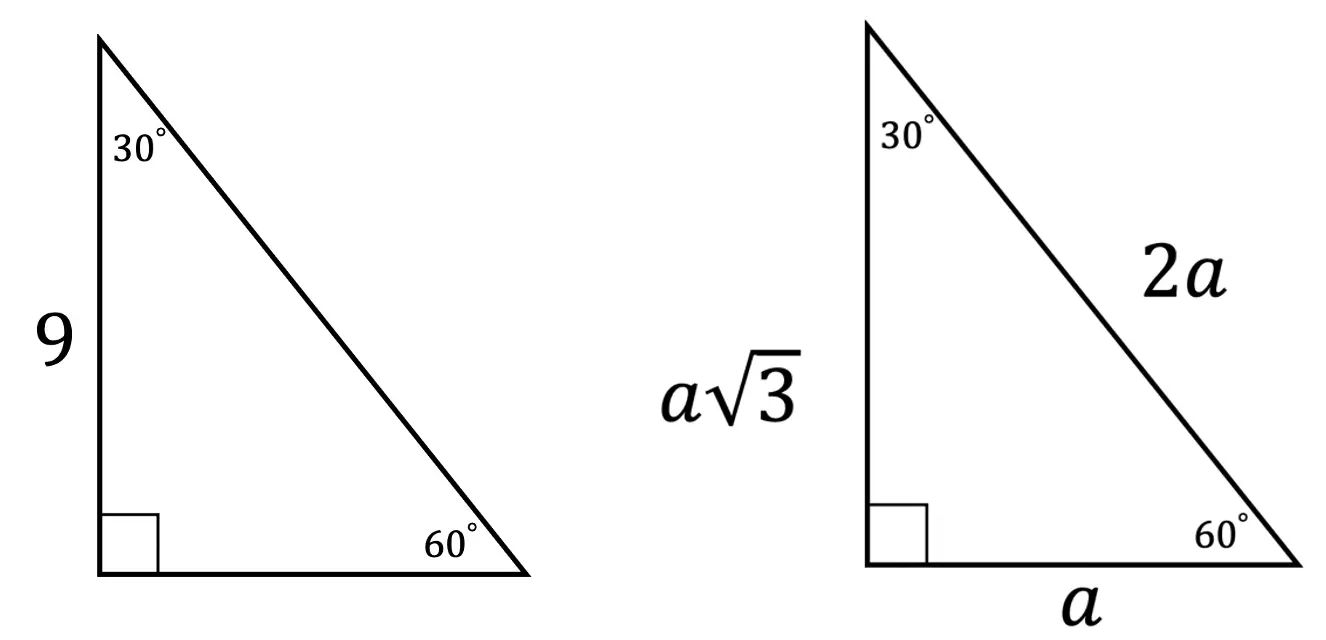



30 60 90 Special Triangles Geometry Mathsux 2




Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube
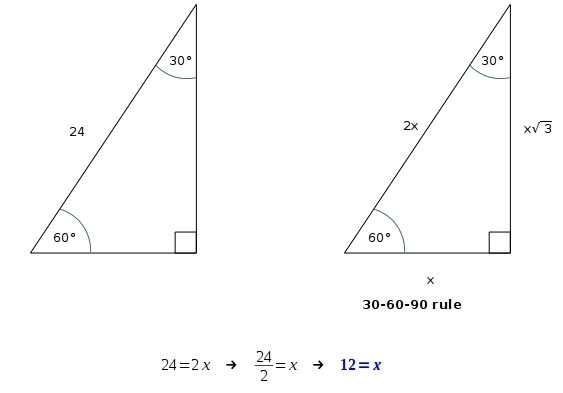



The Length Of The Hypotenuse Of A 30 60 90 Triangle Is 24 What Is The Perimeter
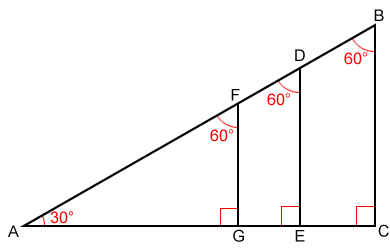



30 60 90 Triangle




30 60 90 Triangle Theorem Ratio Formula Video




Special Right Triangles Review Article Khan Academy



30 60 90 And 45 45 90 Triangle Calculator



1
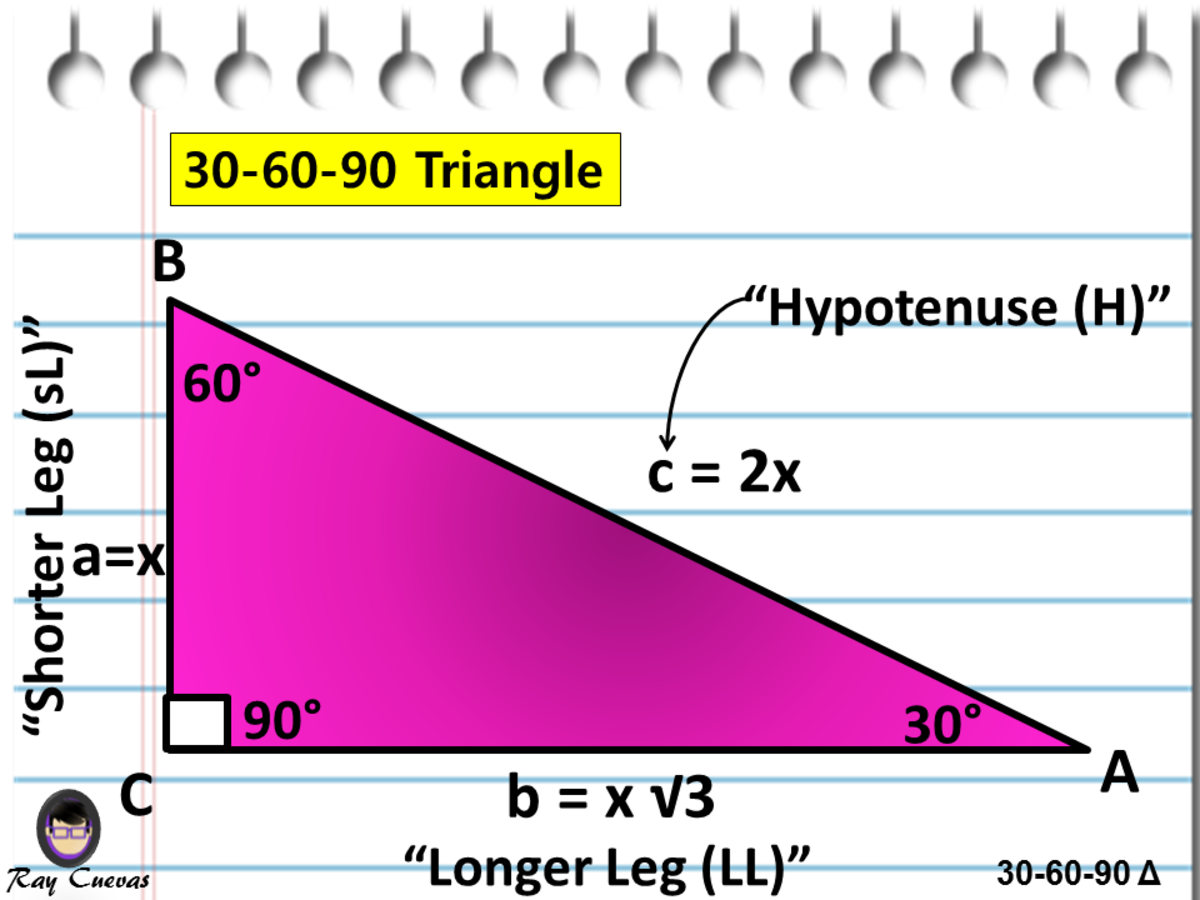



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
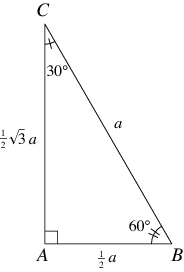



30 60 90 Triangle From Wolfram Mathworld
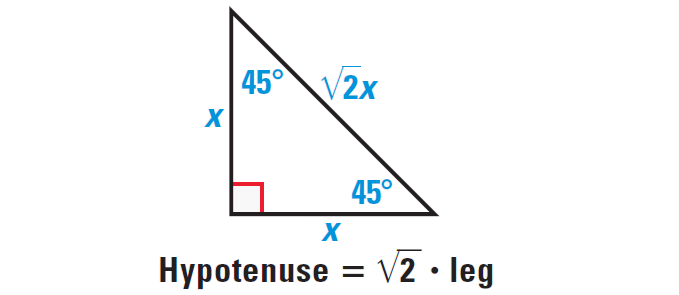



Special Right Triangles



The Easy Guide To The 30 60 90 Triangle




How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies




The Complete Guide To The 30 60 90 Triangle



How Many Triangles Can Be Drawn With Angles 30 60 And 90 Degrees Quora
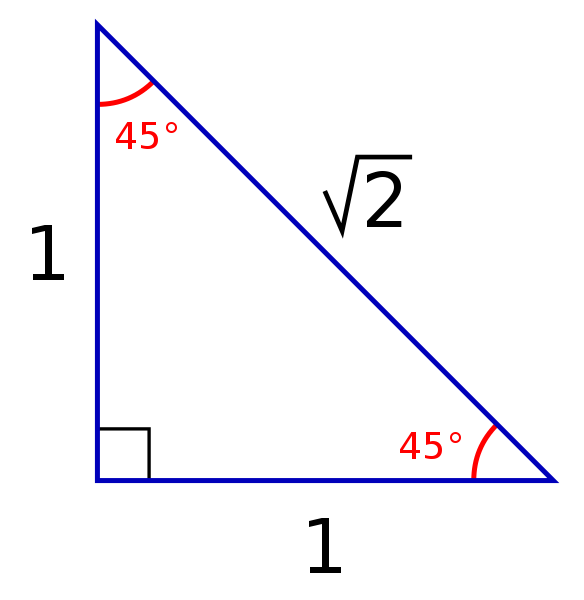



30 60 90 Triangle Formulas Rules And Sides Science Trends



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Proof Don T Memorise Youtube




30 60 90 Triangles Special Right Triangle Trigonometry Youtube




A Quick Guide To The 30 60 90 Degree Triangle Dummies




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
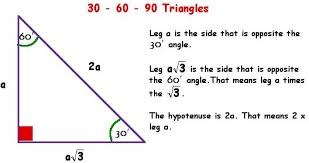



30 60 90 Right Triangle Theorem By Stephanie Joaquin Infographic




30 60 90 Right Triangles Free Math Help




A Quick Guide To The 30 60 90 Degree Triangle Dummies




30 60 90 Triangle Theorem Ratio Formula Video



Fastest What Is The Rule For A 30 60 90 Triangle




30 60 90 Triangle Calculator Formula Rules




30 60 90 Triangle Definition Theorem Formula Examples



5 5 22 Special Right Triangles 30 60 90 Mosley Nc Math 2 Honors S2




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com
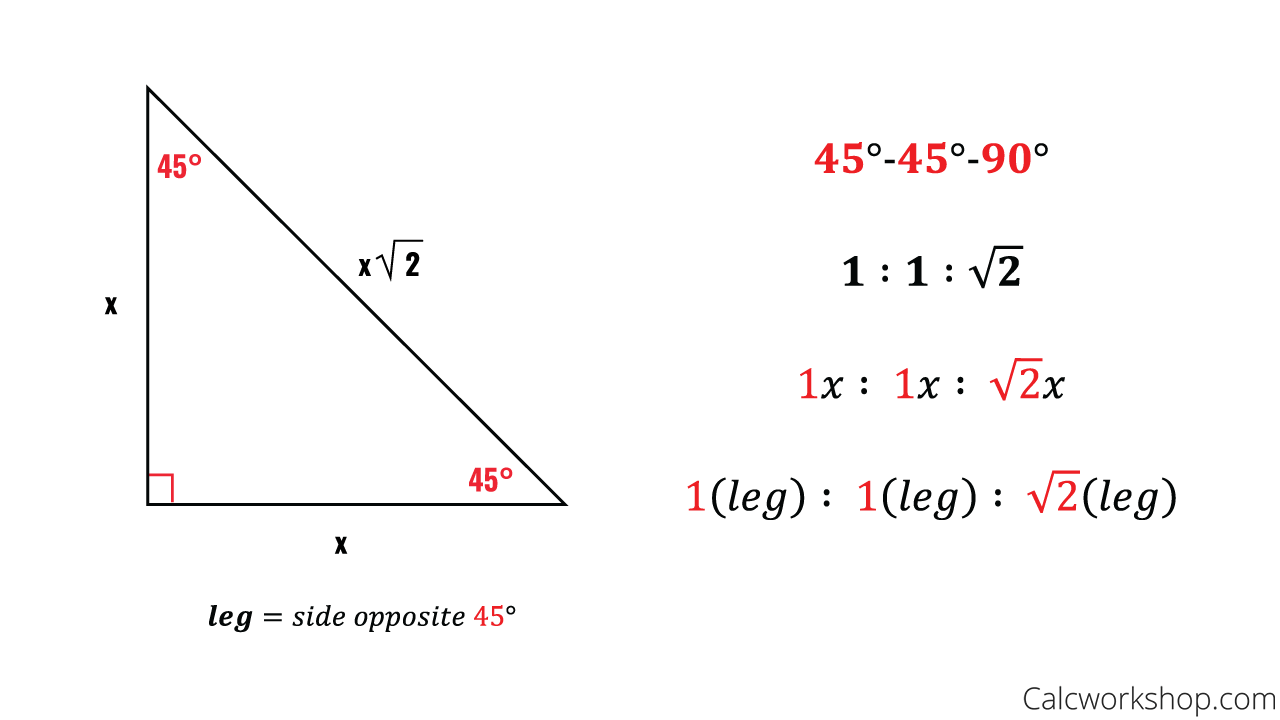



Special Right Triangles Fully Explained W 19 Examples




30 60 90 Triangle Theorem Ratio Formula Video



45 45 90 And 30 60 90 Triangles Zona Land Education
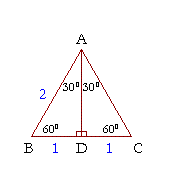



The 30 60 90 Triangle Topics In Trigonometry




30 60 90 45 45 90 Special Right Triangles Free Printable Math Worksheets Teaching Geometry Printable Math Worksheets




30 60 90 Triangle Calculator Formula Rules
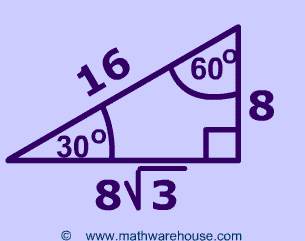



Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Formulas Rules And Sides Science Trends



1
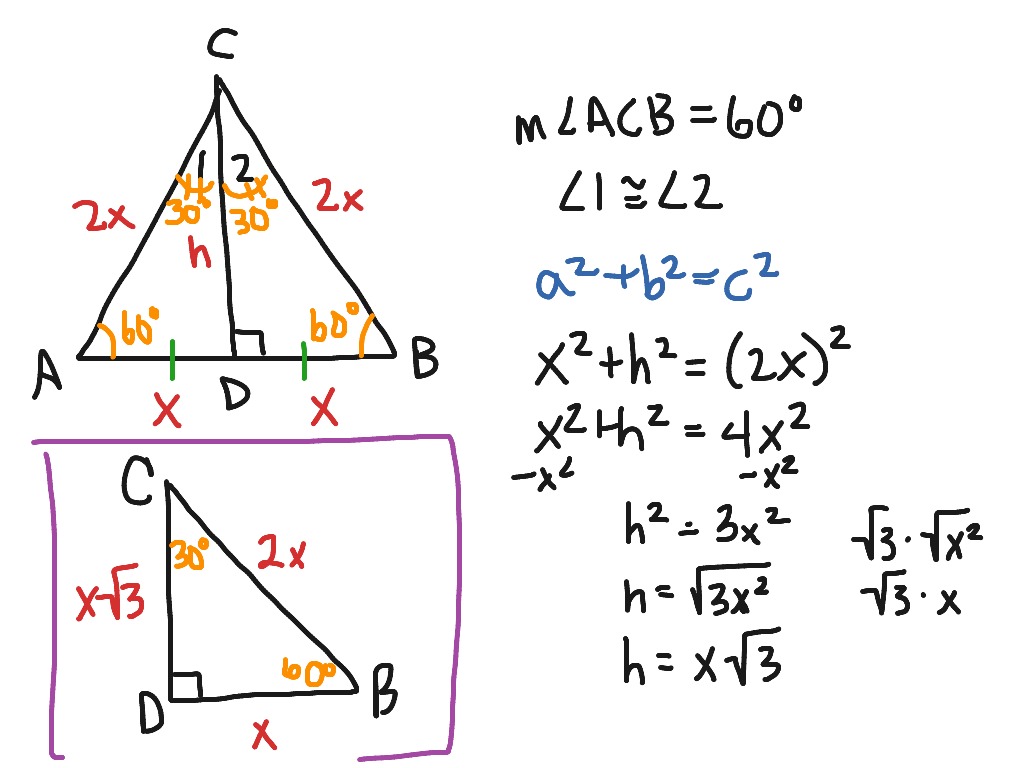



30 60 90 Triangle Math Right Triangles Showme




30 60 90 Triangle Sides Examples Angles Full Lesson




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Right Triangle Side Ratios Expii




30 60 90 Triangle Calculator Formula Rules




Special Right Triangle Wikipedia
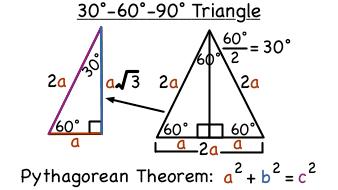



What Is A 30 60 90 Degree Triangle Virtual Nerd




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



5 5 Special Triangles




Learn About The 30 60 90 Triangle Caddell Prep Online



Mrwadeturner 30 60 90 Triangle 6th




Special Right Triangles Gmatsyllabus Com
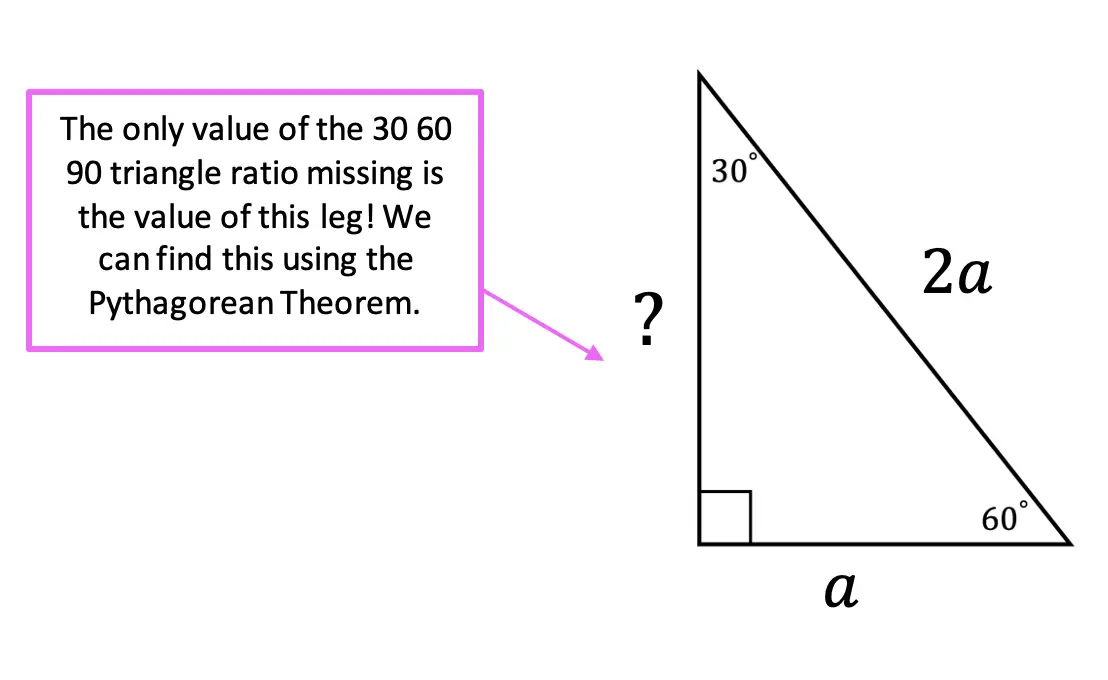



30 60 90 Special Triangles Geometry Mathsux 2




Special Right Triangles Review Article Khan Academy




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Special Right Triangle Calculator Inch Calculator
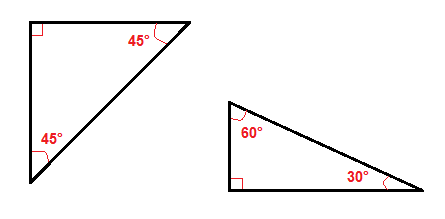



The Pythagorean Theorem Pre Algebra Right Triangles And Algebra Mathplanet
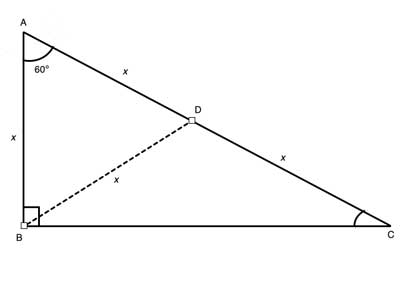



30 60 90 Triangle Geometry Help
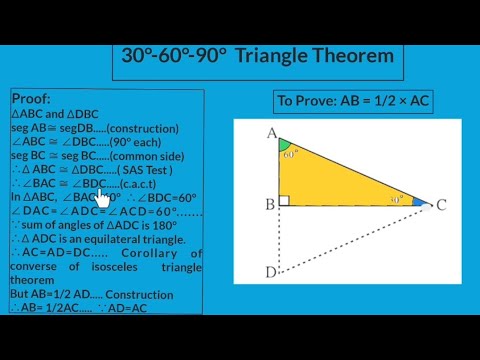



9th Maths 2 30 60 90 Triangle Theorem Youtube



Special Right Triangles Proof




The 30 60 90 Triangle Topics In Trigonometry
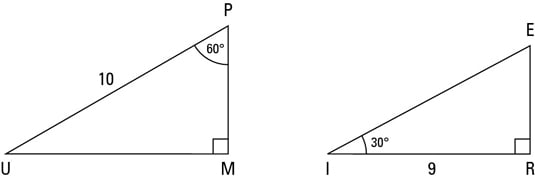



Identifying The 30 60 90 Degree Triangle Dummies




How To Work With 30 60 90 Degree Triangles Education Is Around



1




Special Right Triangles Video Lessons Examples And Solutions




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com



0 件のコメント:
コメントを投稿